
Sportsbook in Canada
Sportsbook in Canada The Best Sportsbook in Canada: Comparing Sports Interaction vs the Competition Sports Interaction was one of the first sportsbooks to open its
There are all types of rating methods online today. One of the most popular is the 5 star rating method. You’ve seen it everywhere from Yelp, to iTunes, to Amazon, to Netflix.
Unfortunately, 5-star rating methods face many challenges in their use, and numerous studies have identified flaws with this particular methodology.
The graph below illustrates the main issue with the 5-star rating scale. Most of the ratings are distributed to the 1 and 5-star ratings. Most people will only comment if they really like or don’t like something. The additional options of 2, 3, and 4 stars are unnecessary.
After learning this, YouTube moved to a thumbs up / thumbs down rating system. However, taking all of the options out might be a bit much. Having a third, middle (the ‘meh’ preference) option in there is good to balance things out.

Sportsbook in Canada The Best Sportsbook in Canada: Comparing Sports Interaction vs the Competition Sports Interaction was one of the first sportsbooks to open its

How to Win at Roulette at the Casino Year’s Guide The game of roulette is one of the most popular in all of the casinos.

Cheat at Roulette: Find out if any well-known roulette cheats are worth trying out. … There are a few legal methods for cheating the casino in live roulette…

The dream of playing ANONYMOUSLY comes true. No personal data will be requested, even for WITHDRAWAL. An email is enough. Unfortunately, they are all only in English. Some are reliable and others less.

Bingo Mathematician Joseph Granville Choose your bingo cards like Joseph Granville Although bingo is categorized as a game of chance, there are certain tricks that

Playing Safe Online Roulette Playing casino games online can be an eye-opening new experience for those who are only used to playing at conventional casinos.
The higher the average, the higher the item is listed in the scale.
For example:
Product A has 10 ratings, 9 of which are 5 stars and 1 is 1 star. Average rating of 4.6 stars.
Product B has 100 ratings, 85 of which are 5 stars and 15 of which are 1 star. Average rating of 4.4 stars.
Product A will be listed above Product B because it has a higher average. However, Product A has significantly fewer ratings and doesn’t necessarily deserve to be ranked above Product B.
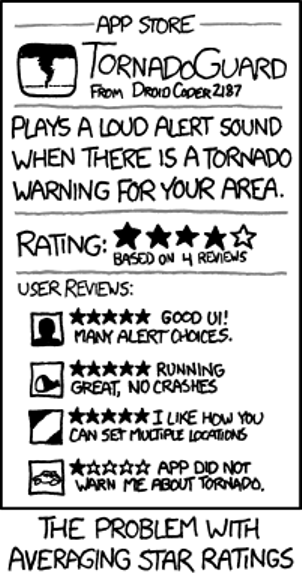
Averages can be misleading and distract you from important details within specific ratings. Sometimes, just 1 review matters. We can’t find a better way to illustrate this point than with this comic from XKCD. This is a comic pretending to display ratings for a ‘Tornado Guard’ app that will alert you when tornados are near. The app has an average rating of 4 stars, but really, it’s only the last review that really matters.
If you were a quarterback and threw the ball one foot too far ahead of your receiver half the time, and one foot too far behind your receiver the other half of the time, you wouldn’t see a lot of playing time. But if we were measuring the accuracy of your throwing, we might conclude that, on average, you were extremely accurate. And that is the basic problem with averages: they can hide what you need to know.
Averages are simple to calculate and are sometimes a lazy way of determining past performance. For example, over some period of time, a performance level may have started at 50% and ended up at 70%. Simple math then determines the average to be 60%, so 60% is now used as a baseline to measure future performance against.
If the next performance level measured is 65%, you might conclude that performance has improved, which it has over the baseline. But in fact, it has degraded from the true starting point of 70%. Your next decisions could lead you in the wrong direction.
Averages are easy to manipulate. The simplest way to manipulate averages is to change the base period or exclude the “outliers,” which are those data points that seem to be abnormally high or low when compared with the majority. One of our clients once told us that the key to understanding what drives performance is not to exclude outliers but to study them.
By looking at the best and worst months over the last year, he learned what most impacted his results. Another outlier study we learned about (from the automotive industry) is a concept called BOB WOW, which stands for best-of-the-best and worst-of-the-worst. This one we find effective for looking at variances in individual performance. Studying the outliers gives insight into what helps or hinders success.
In one retail project we did for a shoe manufacturer we observed the company’s most and least successful salespeople. We found the simple act of getting people to try on shoes had a marked impact on their likelihood to purchase. The sales reps couldn’t specifically articulate it, but their greeting, questions, and even movement were designed to get you to invest time and energy in putting on shoes. Over time they intuitively knew that one action led to better odds of making a sale.
Consider the case of the statistician who drowns while fording a river that he calculates is, on average, three feet deep. If he were alive to tell the tale, he would expound on the “flaw of averages,” which states, simply, that plans based on assumptions about average conditions usually go wrong. This basic but almost always unseen flaw shows up everywhere in business, distorting accounts, undermining forecasts, and dooming apparently well-considered projects to disappointing results.
Let’s say that a company I’ll call HealthCeuticals sells a perishable antibiotic. Although demand for the drug varies, for years the average monthly demand has been 5,000 units, so that’s the quantity the company currently stocks. One day, the boss appears. “Give me a forecast of demand for next year,” he says to his product manager. “I need it to estimate inventory cost for the budget.” The product manager responds, “Demand varies from month to month. Here, let me give you a distribution.” But the boss doesn’t want a “distribution.” “Give me a number!” he insists. “Well,” the manager says meekly, “the average demand is 5,000 units a month. So, if you need a single number, go with 5,000.”
The boss now proceeds to estimate inventory costs, which are calculated as follows: If monthly demand is less than the amount stocked, the firm incurs a spoilage cost of $50 per unsold unit. On the other hand, if the demand is greater than the amount stocked, the firm must air-freight the extra units at an increased cost of $150 each. These are the only two costs that depend on the accuracy of the forecast. The boss has developed a spreadsheet model to calculate the costs associated with any given demand and amount stocked. Since the average demand is 5,000 units, he plugs in 5,000. Since the company always stocks 5,000 units, the spreadsheet dutifully reports that for this average demand, the cost is zero: no spoilage or airfreight costs.
A bottom line based on average assumptions should be the average bottom line, right? It may miss fluctuations from month to month, but shouldn’t you at least get the correct average cost by plugging in average demand? No. It’s easy to see that the average cost can’t be zero by noting that when demand for HealthCeuticals’ antibiotic deviates either up or down from the average, the company incurs costs.
Executives’ desire to work with “a number,” to plug in an average figure, is legendary. But whenever an average is used to represent an uncertain quantity, it ends up distorting the results because it ignores the impact of the inevitable variations. Averages routinely gum up accounting, investments, sales, production planning, even weather forecasting. Even the Generally Accepted Accounting Principles sanction the “flaw,” requiring that uncertainties such as bad debt be entered a s single numbers. (To its credit, the SEC has proposed new rules that would begin to address this problem.)
In one celebrated, real-life case, relying on averages forced Orange County, California, into insolvency. In the summer of 1994, interest rates were low and were expected to remain so. Officials painted a rosy picture of the county’s financial portfolio based on this expected future behavior of interest rates. But had they explicitly considered the well-documented range of interest-rate uncertainties, instead of a single, average interest-rate scenario, they would have seen that there was a 5% chance of losing $1 billion or more—which is exactly what happened. The average hid the enormous riskiness of their investments.
More recently, a failure to appreciate the flaw led to $2 billion in property damage in North Dakota. In 1997, the U.S. Weather Service forecast that North Dakota’s rising Red River would crest at 49 feet.
Officials in Grand Forks made flood management plans based on this single figure, which represented an average. In fact, the river crested above 50 feet, breaching the dikes, and unleashing a flood that forced 50,000 people from their homes.
Some executives are already attuned to the importance of acting on a range of relevant numbers—a distribution—rather than single values, and they employ statisticians who estimate the distributions of everything from stock prices to electricity demand. Increasingly, companies are also turning to software-based cures for the flaw.
Many programs now simulate uncertainty, generating thousands of possible values for a given scenario—in essence, replacing the low-resolution “snapshot” of a single average number with a detailed “movie.” The movie comprises a whole range of possible values and their likelihood of occurring—the frequency distribution.
The simplest and most popular tool, called the Monte Carlo simulation, was described by David Hertz in a 1964 HBR article and popularized in financial circles by sophisticated users like Merck CFO and executive vice president Judy Lewent. Today, spreadsheet-based Monte Carlo simulation software is widely available and is being used in fields as diverse as petroleum exploration, financial engineering, defense, banking, and retirement portfolio planning.
Wells Fargo Bank, for instance, used a Monte Carlo simulation to predict the cost of offering customers a variable-rate CD, whose return would increase if interest rates rose. A previous estimate based on three years of 1990s interest-rate data had shown that the cost would be about 0.10% for a five-year CD.
But the Monte Carlo simulation, which combined interest-rate data going back to 1965 with models of customer behavior, found that the bank’s cost could be eight times that amount. The alarming finding induced the bank to reconfigure its CD product to reduce the chance of unacceptable costs should interest rates rise.
Had the average-obsessed boss at HealthCeuticals used Monte Carlo simulation, he would have seen not only that the average inventory cost was not zero but that he shouldn’t have been stocking 5,000 units in the first place. For executives like him who are still fond of single values, it’s time for a shift in mindset. Rather than “Give me a number for my report,” what every executive should be saying is “Give me a distribution for my simulation.”